Absolute Value Equations

The absolute value of a number x is the distance from x to 0 on the real number line and is written as |x|. The absolute value function can be written as a "piecewise-defined function". Therefore, when solving absolute value equations, you need to consider 2 cases. The first case considers what happens when x is positive and the second is when x is negative. 

|x|= x if x > 0

|x|= - x if x < 0

Solving Equations and Inequalities

When solving equations or inequalities that involve absolute value, the following three principles will be useful. Notice that you will be required to solve two separate parts corresponding to two different cases. The first step is to separate the equation or inequality into it's two cases and remove the absolute value signs. The second step is to solve the equations or inequalities as usual.

If a > 0, then

• |x| = a if and only if x = ± a;
• |x| < a if and only if - a < x < a; and
• |x| > a if and only if x > a or x < -a.

Example: Solve \( |x-8|=4 \) for \(x\).

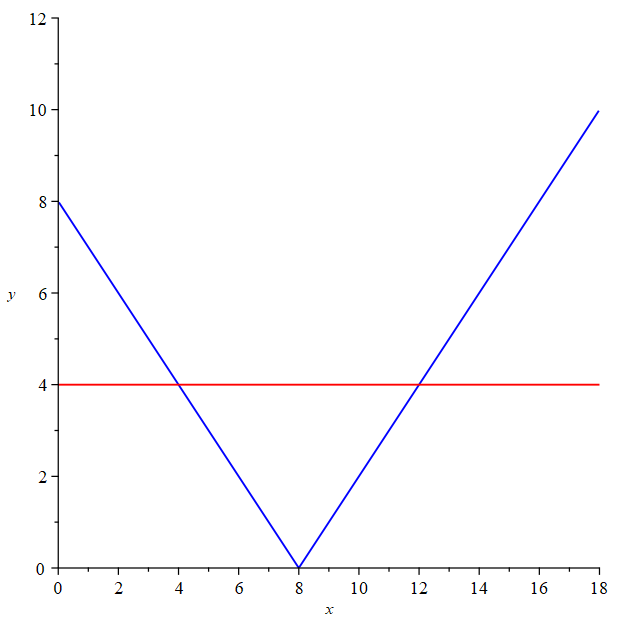
 Solution: 

        \(x-8=4\)         or                \(x-8=-4\)

               \(x=12\)                                  \(x=4\)

Therefore, \(x=4, 12\).

Example: Solve |x + 5| < 1 for x.

Solution:

-1 < x + 5 < 1

-1 < x + 5                           x + 5 < 1

-6 < x                                        x < -4

Therefore, -6 < x < -4. 

Example: