Parabolas
A parabola is a conic section. The following two plots are examples of parabolas:
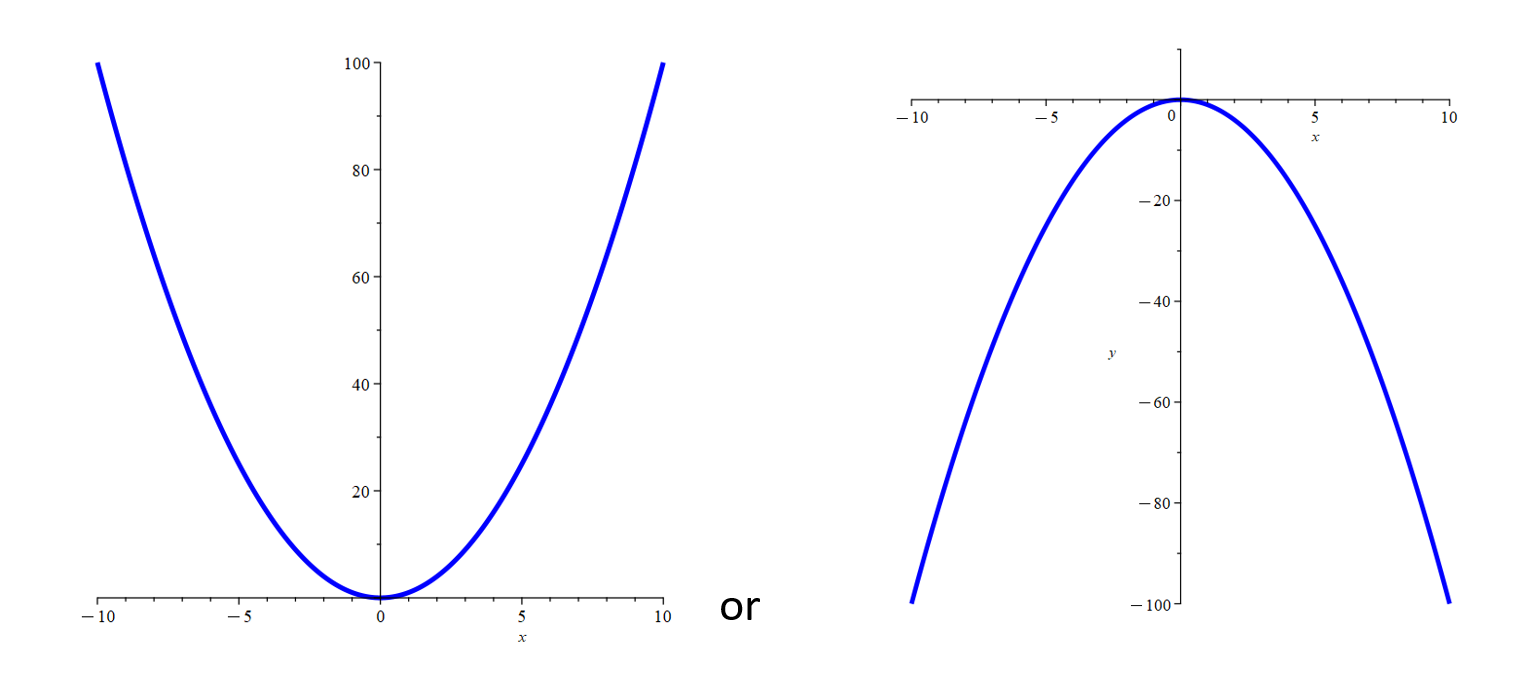
Parabolas have the property that when transformed (stretched/compressed) along a direction parallel or perpendicular to its axis, the curve remains a parabola. For example, a line also has this property, but a circle does not. If a line is stretched or compressed, it retains its shape; a circle does not.
Any function of the form f(x) = a(x - h)2 + k is in the square family because it is a transformation of f(x) = x2. The graph of any function in the square family is called a parabola. Therefore, the graph of any quadratic function is a parabola.
Opening and Vertex of a Parabola
There are two forms of the quadratic function, where one form is f(x) = a(x - h)2 + k and the other form is f(x) = ax2 + bx + c. If a > 0, the graph of f(x) = a(x - h)2 + k opens upward; if a < 0, the graph opens downward. This rule is illustrated by the above two plots.
We can find the vertex of the parabola when the function is written in either form.
- For a quadratic function in the form f(x) = a(x - h)2 + k, the vertex of the parabola is (h, k).
- For the form f(x) = ax2 + bx + c, the x-coordinates of the vertex is -b/2a and the y-coordinate of the vertex is f(-b/2a).
Example: Find the vertex for each parabola: f(x) = -2(x + 4)2 -8 and f(x) = 2x2 - 4x -9.
Solution one: For f(x) = -2(x + 4)2 -8:
The parabola follows: f(x) = a(x - h)2 + k, so the vertex is (h, k) = (-4, -8).
Solution two: For f(x) = 2x2 - 4x -9:
The parabola follows f(x) = ax2 + bx + c, so the x-coordinate of the vertex is -b/2a = 4/4 = 1 and y-coordinate is f(-b/2a) = f(1) = 2(1)2 - 4(1) - 9 = -11. So the vertex is (1, 11).
Intercepts
The x- and y-intercepts are important points on the graph of a parabola. The y-intercept(s) are easily found by letting x = 0. The x-intercepts are found by letting y = 0 and solving the resulting equation.
Example: Find the y-intercept(s) and the x-intercept(s) for the parabolas f(x) = -2(x + 4)2 -8 and f(x) = 2x2 - 4x -9.
Solution one: For f(x) = -2(x + 4)2 -8:
If x = 0, then y = -2(0 + 4)2 -8 = -40. The y-intercept is (0, 40).
There are no x-intercepts. Since a< 0, the parabola opens downward and from our vertex example above, our vertex is (-4, -8), which is below the x-axis. If we set y = 0 and solve for x, we get -4 = (x + 4)2, which has no real solution.
Solution two: For f(x) = 2x2 - 4x -9:
If x = 0, then y = 2(0)2 - 4(0) -9 = -9. The y-intercept is (0, -9).
Since a > 0, the parabola opens upward and from our vertex example above, our vertex is (1, -11), which is below the x-axis. Set y = 0 and solve for 0 = 2x2 - 4x -9.
Using the quadratic equation:
\(x=\frac{-b\pm\sqrt{b^2-4ac}}{2a} = \frac{4\pm \sqrt{(-4)^2 - 4(2)(-9)}}{2(2)} = \frac{4\pm\sqrt{88}}{4} = \frac{2\pm\sqrt{22}}{2}\)
Therefore, the x-intercepts are:
\(\left(\frac{2-\sqrt{22}}{2},0\right)\text{ and }\left(\frac{2+\sqrt{22}}{2},0\right)\)
Example:
