Transformations of Trigonometric Functions

The transformation of functions includes the shifting, stretching, and reflecting of their graph. The same rules apply when transforming trigonometric functions.

Vertical and Horizontal Shifts

Suppose c > 0. To obtain the graph of

$y = f(x) + c$: shift the graph of $y = f(x)$ up by $c$ units

$y = f(x) - c$: shift the graph of $y = f(x)$ down by $c$ units

$y = f(x - c)$: shift the graph of $y = f(x)$ to the right by $c$ units

$y = f(x + c)$: shift the graph of $y = f(x)$ to the left by $c$ units

Example: Sketch the function $y=\sin(x), y=\sin(x)+4,$ and $y=\sin(x+\frac{\pi}{2})$.

Solution:

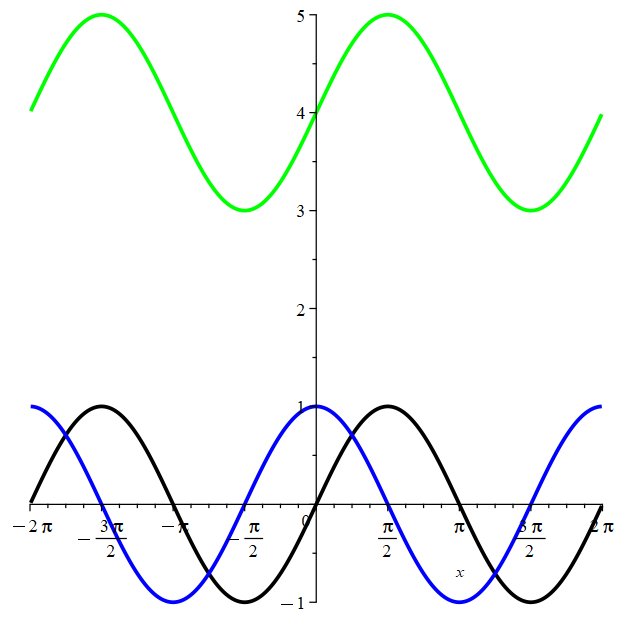
$graphs of sin(x) with vertical and horizontal shifts$

Here, $y=\sin(x)$ is shown in black. The curve $y=\sin(x)+4$ is shifted 4 units up, shown in green. The curve $y=\sin(x+\frac{\pi}{2})$ is shifted $\frac{\pi}{2}$ units to the left, and is shown in blue. Notice that this is the same thing as the curve $y=\cos(x)$.

Vertical and Horizontal Stretches/Compressions

Suppose c > 1. To obtain the graph of

$y = cf(x)$: stretch the graph of $y = f(x)$ vertically by a factor of $c$

$y = \frac{1}{c} f(x)$: compress the graph of $y = f(x)$ vertically by a factor of $c$

$y = f(cx)$: compress the graph of $y = f(x)$ horizontally by a factor of $c$

$y = f(\frac{x}{c})$: stretch the graph of $y = f(x)$ horizontally by a factor of $c$

Example: Sketch the functions $y=\cos(x), y=\cos(2x),$ and $y=3\cos(2x)$.

Solution:

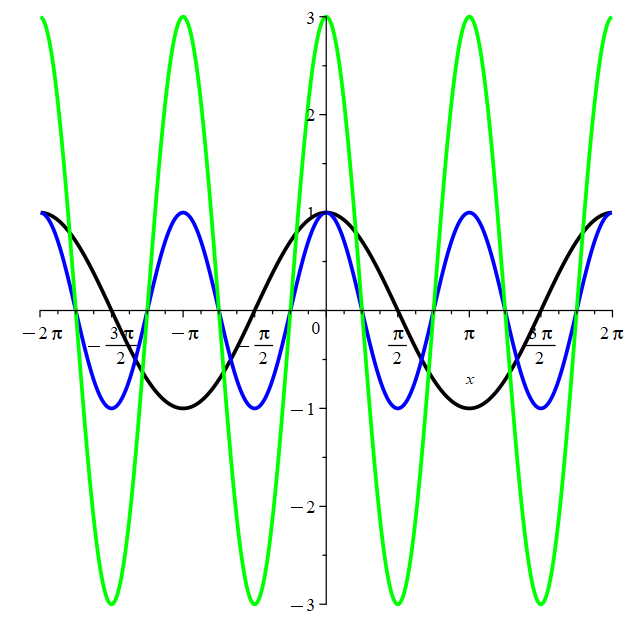
$cosine graph with horizontal compression and vertical stretch$

The function$y=\cos(x)$ is shown in black. The blue curve represents the function $y=\cos(2x)$ and is compressed horizontally by a factor of 2. The green curve represents the function $y=3\cos(2x)$ and is the blue curve stretched vertically by a factor of 3.

Reflections

To obtain the graph of

$y = -f(x)$: reflect the graph of $y = f(x)$ about the x-axis; and

$y = f(-x)$: reflect the graph of $y = f(x)$ about the y-axis

Example: Given that the blue curve represents the function $y=\sin(x)$, determine whether the following statement is TRUE or FALSE.

The green curve on the following graph represents both $y=-\sin(x)$ and $y=\sin(-x)$.

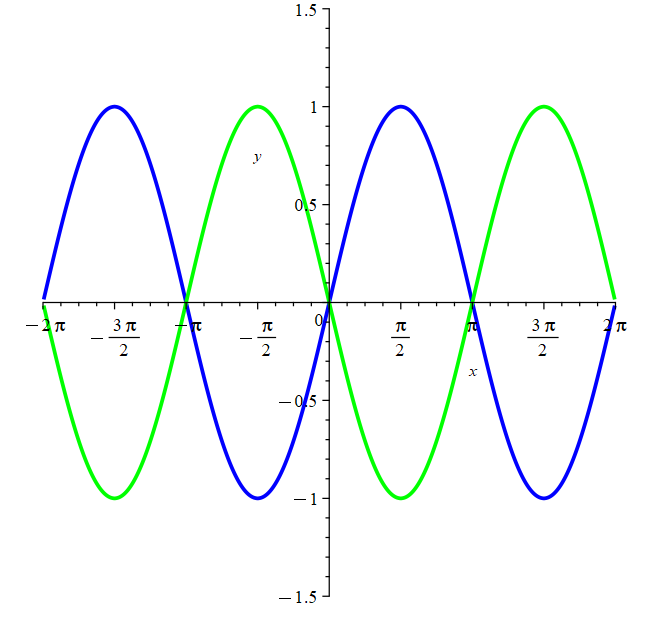
$sine graph reflected in x-axis and y-axis$

Solution: TRUE - The green curve does represent $y=-\sin(x)$ and $y=\sin(-x)$. In this particular situation the reflection about the x-axis is the same as the reflection about the y-axis.

Example 1:

Example 2: