Trigonometry on the Unit Circle
The unit circle
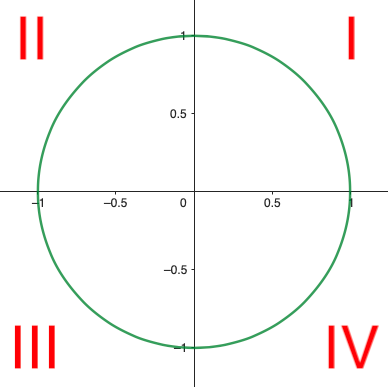
To help us understand the geometric meaning of the trigonometric functions, it is helpful to consider what \(\sin \theta\) and \(\cos \theta\) represent on the unit circle. A unit circle is a circle with radius 1 that is centered at the origin (i.e. this circle would have the equation \(x^2 + y^2 = 1\)). The 4 quadrants are as labeled below. Angles are measured counter-clockwise starting from the positive \(x\)-axis.
CAST rule
The CAST rule is used to help you remember the quadrants in which \(\sin(\theta) \) \(\cos(\theta)\) and \(\tan(\theta)\) are positive.
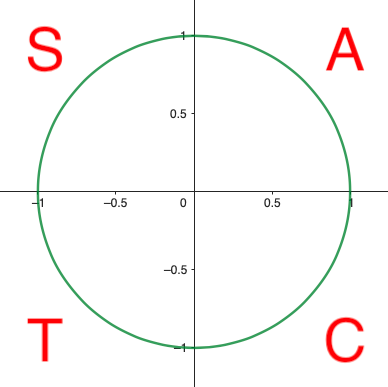
Quadrant 1 is represented by A therefore all three are positive in that quadrant.
Quadrant 2 is represented by S therefore \(\sin(\theta) \) is positive in that quadrant.
Quadrant 3 is represented by T therefore \(\tan(\theta)\) is positive in that quadrant.
Quadrant 4 is represented by C therefore \(\cos(\theta)\) is positive in that quadrant.
SOH CAH TOA and special angles
In trigonometry there are special angles at which you should know the value of the various trigonometric functions. The two special triangles below can be used to help you find these values, but first we need to remember how sine and cosine are defined based on the sides of a right angle triangle. To help us remember we use:
\[ \sin \theta = \frac{\text{opposite}}{\text{hypotenuse}} \quad \cos\theta = \frac{\text{adjacent}}{\text{hypotenuse}} \quad \tan\theta = \frac{\text{opposite}}{\text{adjacent}} \]
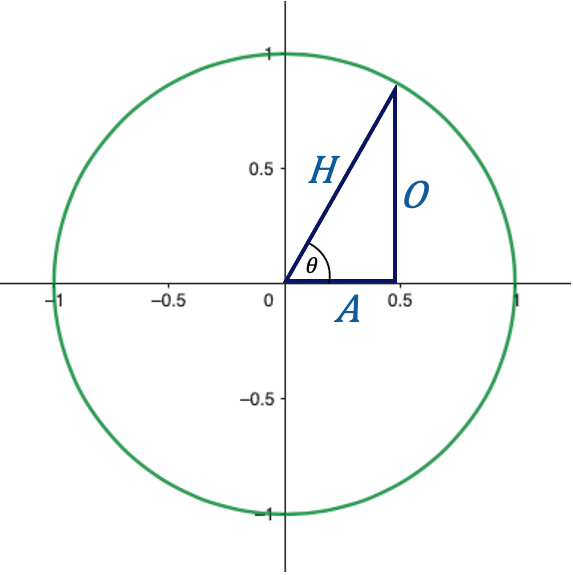
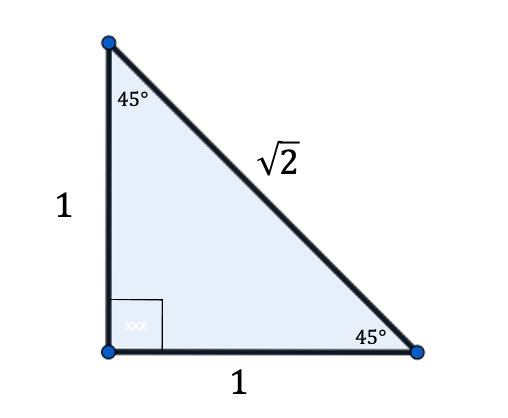
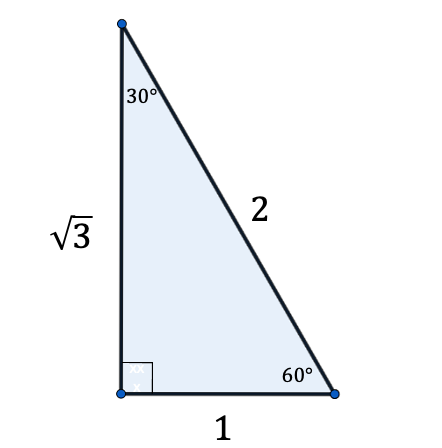
Using the above triangles and SOHCAHTOA, we end up with the following chart (note that the angles in the chart below are given in units of radians):
| \[\theta\] | \[0\] | \[\frac{\pi}{6}\] | \[\frac{\pi}{4}\] | \[\frac{\pi}{3}\] | \[\frac{\pi}{2}\] |
| \[\sin(\theta)\] | \[0\] | \[\frac{1}{2}\] | \[\frac{1}{\sqrt{2}}\] | \[\frac{\sqrt{3}}{2}\] | \[1\] |
| \[\cos(\theta)\] | \[1\] | \[\frac{\sqrt{3}}{2}\] | \[\frac{1}{\sqrt{2}}\] | \[\frac{1}{2}\] | \[0\] |
| \[\tan(\theta)\] | \[0\] | \[\frac{1}{\sqrt{3}}\] | \[1\] | \[\sqrt{3}\] | Undefined |
These values can be used to find the values for \(\csc(\theta), \sec(\theta), \cot(\theta)\) and can also be used with the unit circle below (or CAST rule) to find values in other quadrants.
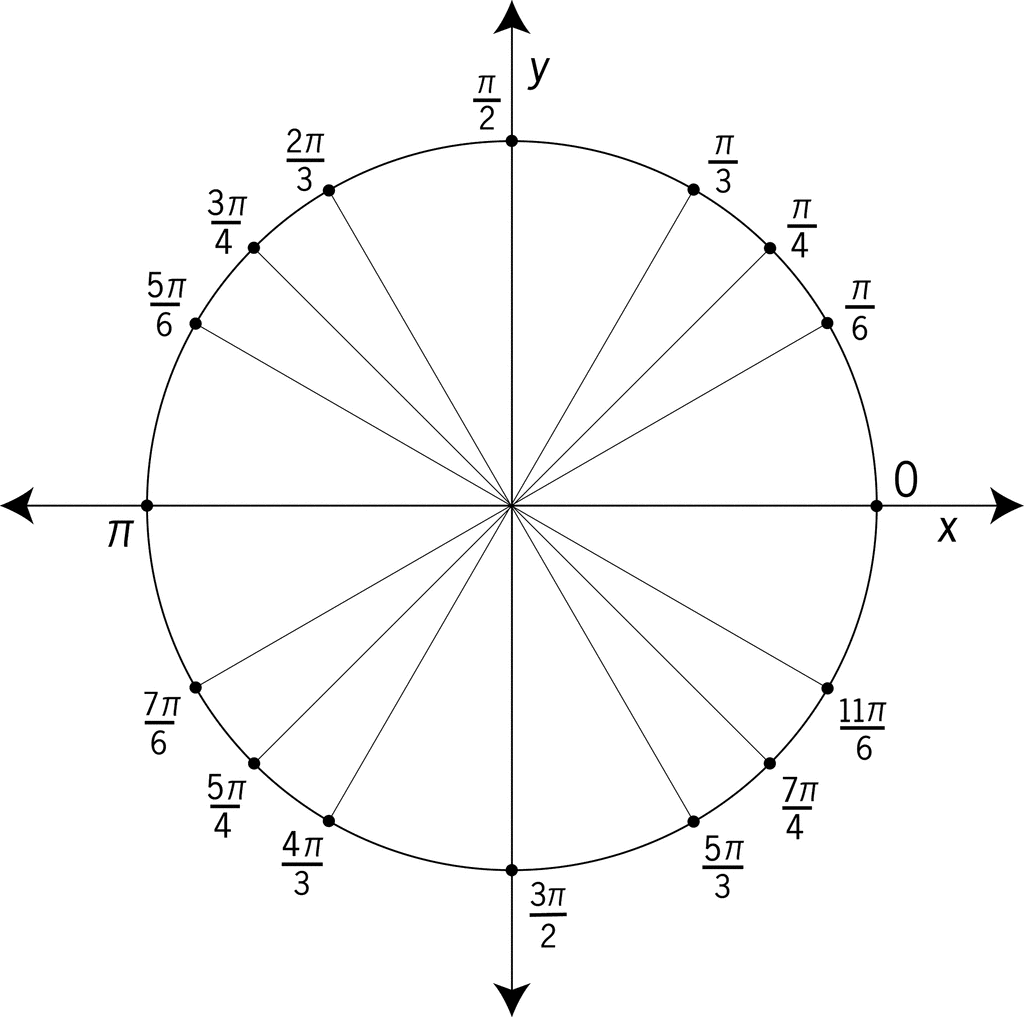
Example: Evaluate \(\cos(\frac{5\pi}{6})\).
Solution: First of all, \(\frac{5\pi}{6} \) is in the second quadrant so cosine has a negative value. Next, use the unit circle to determine that \(\frac{5\pi}{6} \) is related to the angle \(\frac{\pi}{6} \). Finally using the special triangle, \(\cos(\frac{\pi}{6})=\frac{\sqrt{3}}{2}. \) Therefore, \(\cos(\frac{5\pi}{6})=-\frac{\sqrt{3}}{2}. \)
Example: Evaluate \(\csc(\frac{5\pi}{4})\).
Solution: First, we know, \(\frac{5\pi}{4} \) is in the third quadrant so sine has a negative value; consequently, cosecant will also have a negative value. Next, use the unit circle to determine that \(\frac{5\pi}{4} \) is related to the angle \(\frac{\pi}{4} \). Finally using the special triangle, \(\sin(\frac{\pi}{4})=\frac{1}{\sqrt{2}} \) so \(\sin(\frac{5\pi}{4})=-\frac{1}{\sqrt{2}} \) . Therefore, \(\csc(\frac{5\pi}{4})=-\sqrt{2}. \)
Example one:
Example two:
