Solving Trigonometric Equations

INTRO

At this point, you should already be familiar with finding the sine or cosine of an angle. Now, let's turn our attention to finding angles that satisfy a trigonometric equation. Let's look at an example of this graphically.

The red curve below represents the function $y = \sin{(x)} $ and the blue curve represents the line $y=1/2$. Every point at which the blue line intersects the red curve represents a solution of $\sin{(x)} =1/2$. Notice how in just this short interval depicted in the graph there are 8 different solutions for $x$.

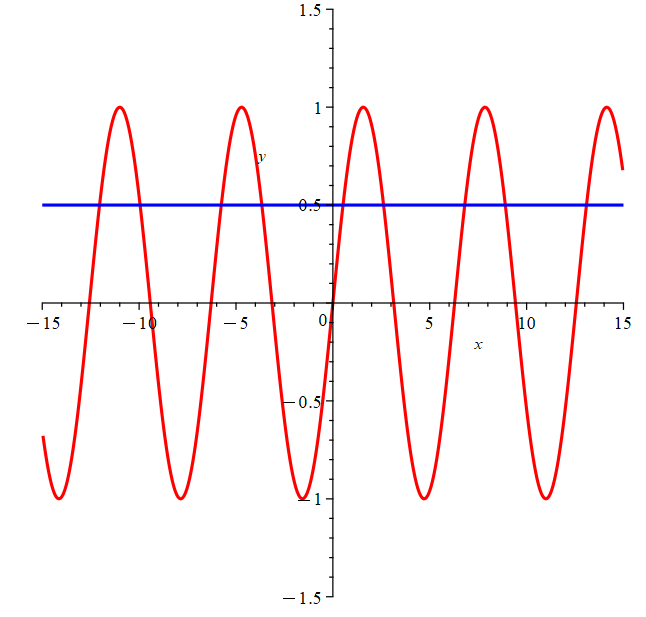
$graph of y=sin(x) and y=1/2$

Depending on whether the right-hand side of the equation is a positive or negative number will determine which quadrants the angles will be in. Since the question above is dealing with sine and the right-hand side is positive, we know that all the solutions for $x$ will be angles in the first and second quadrant. Then using the special triangles and unit circle, we can determine the possible values of $x$.

Example: Solve $\sin(x) = \frac{1}{2}$ for $x$ on the interval $ [-2\pi,2\pi]$.

Solution: $x = \frac{\pi}{6}, \frac{5\pi}{6}$. Note, that we are using units of radians (since the interval is also in radians).

Also, we can find these angles going clockwise:

$x = \frac{-7\pi}{6}, \frac{-11\pi}{6}$.

Example: Solve $\cos(\frac{x}{2}) = 1$ for $x$.

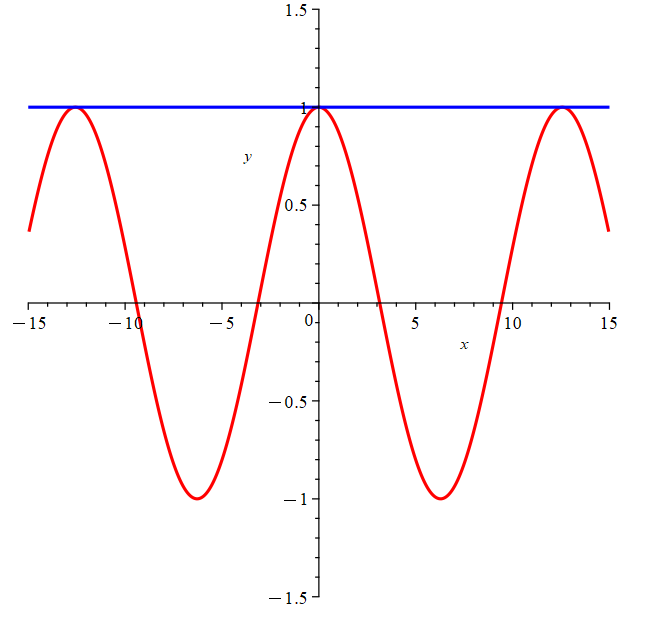
$graphs of y=cos(x/2) and y=1$

Solution: $\cos(\frac{x}{2}) = 1$.

So $(\frac{x}{2}) = 2n\pi$ where we have chosen to solve for $x$ in units of radians.

Consequently, $x = 4n\pi$, where $n$ is any integer.

Example 1:

Example 2:

Example 3: