One-to-One and Onto Functions

 The concept of one-to-one functions is necessary to understand the concept of inverse functions.

One-to-one Functions

If a function has no two ordered pairs with different first coordinates and the same second coordinate, then the function is called one-to-one. This sounds confusing, so let’s consider the following:

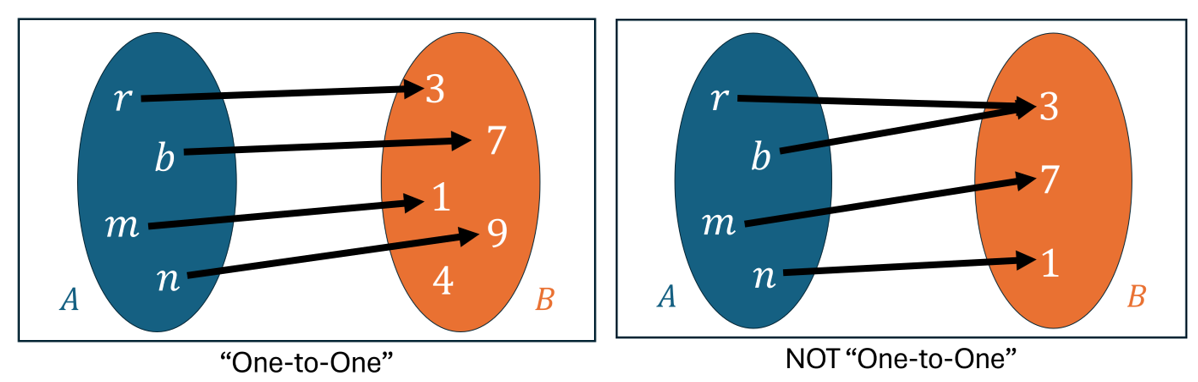
In a one-to-one function, given any y there is only one x that can be paired with the given y.

A graph of a function can also be used to determine whether a function is one-to-one using the horizontal line test:

If each horizontal line crosses the graph of a function at no more than one point, then the function is one-to-one.

Consider the graphs of the following two functions:

 

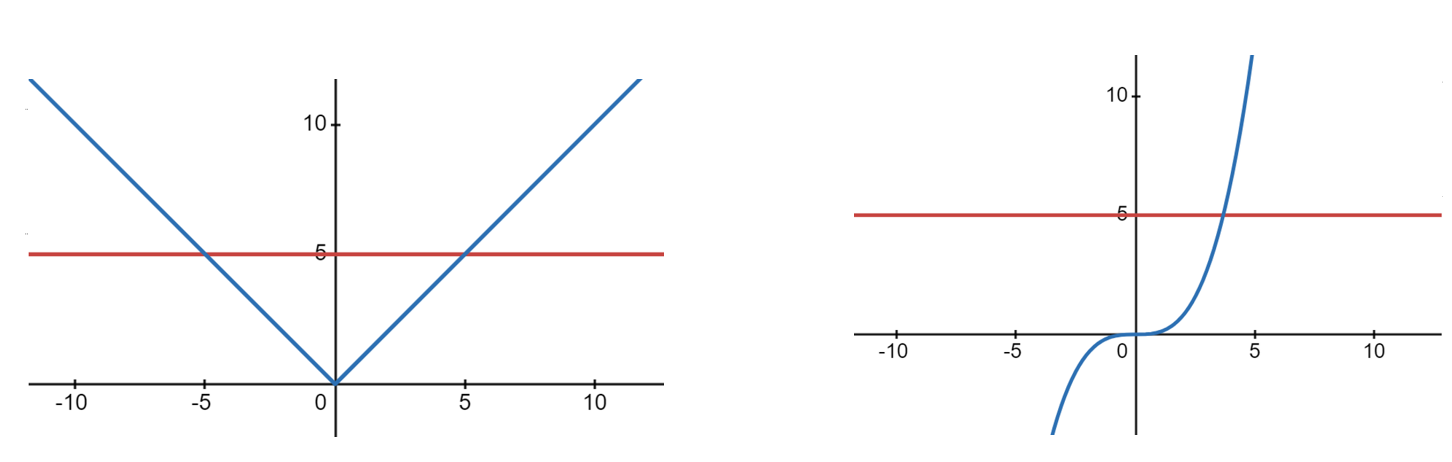
In each plot, the function is in blue and the horizontal line is in red. For the first plot (on the left), the function is not one-to-one since it is possible to draw a horizontal line that crosses the graph twice. However, the second plot (on the right) is a one-to-one function since it appears to be impossible to draw a horizontal line that crosses the graph more than once.

Example: Determine whether the following function is one-to-one:

f = {(1,2), (3, 4), (5, 6), (8, 6), (10, -1)}

Solution: This function is not one-to-one since the ordered pairs (5, 6) and (8, 6) have different first coordinates and the same second coordinate.

Onto functions

An onto function is such that for every element in the codomain there exists an element in domain which maps to it. Again, this sounds confusing, so let’s consider the following:

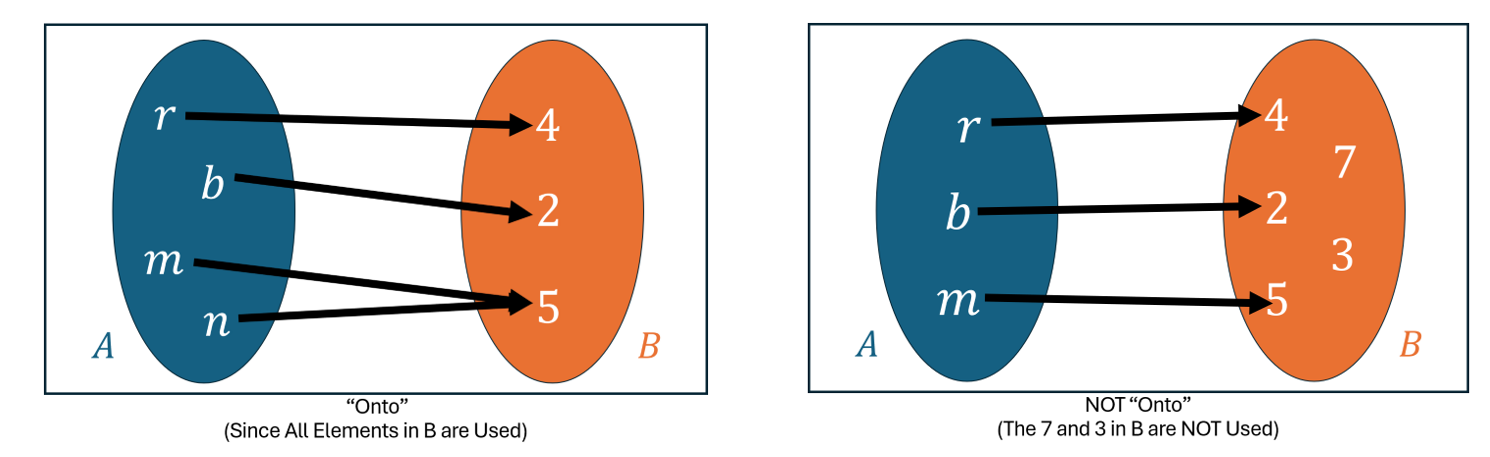
A function f from A to B is called onto if for all b in B there is an a in A such that f(a) = b. That is, all elements in B are used.