Introduction to Functions

Let’s review some background material that you will need to study functions!

Definition of a function

Before we can begin to evaluate and work with functions, it is important to understand what a function is. Functions arise when one quantity is dependent on another. A function f is a rule that assigns to each element from one set exactly one element from another set.

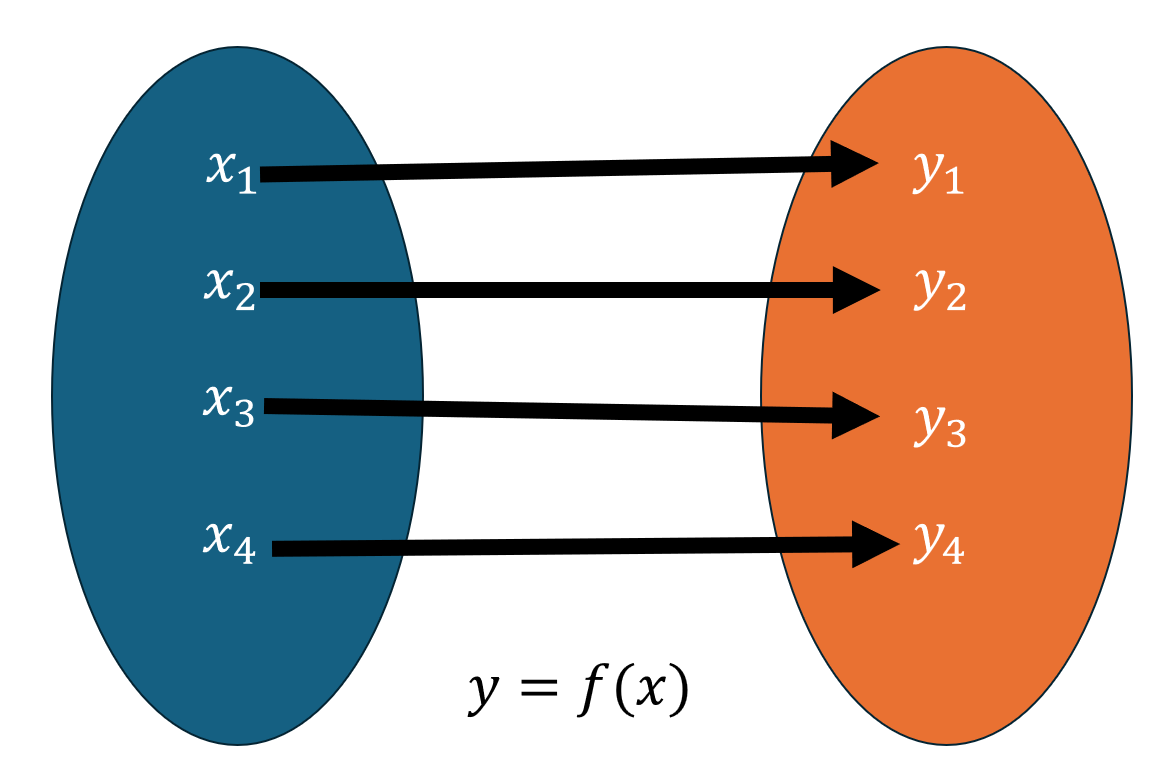
There are 4 ways that a function can be represented:

1. Verbally by a description in words.
2. Numerically by a table of values.
3. Graphically or visually using a graph.
4. Algebraically by an equation.

Vertical Line Test

All relationships are not necessarily functions. Remember that we want each element in the first set to correspond to only one element in the second set. One method for testing to determine if a relationship is a function is the vertical line test. If a vertical line intersects a graph at more than one point, then the graph is not the graph of a function.

Example: Use the vertical line test to determine if the following graphs represent functions.

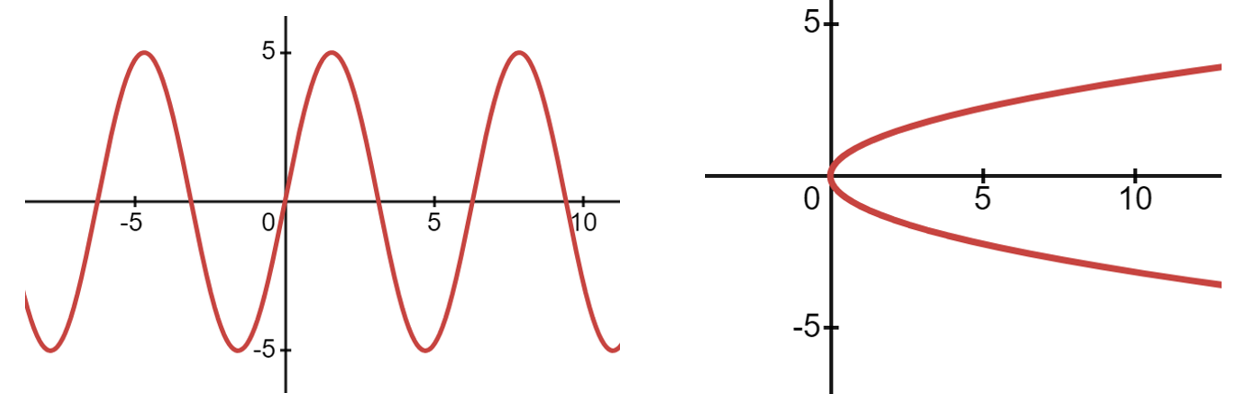
Solution: The figure on the left is an example of a function because no vertical line can intersect the graph at more than one point (assuming the same periodic behavior continues). The figure on the right is not an example of a function because there are many vertical lines that could be drawn that would intersect the graph at two points. 

Function Notation

In many cases, a function will be written in the form of an equation, such as f(x) = 3x + 6 where f(x) is read “f of x”. Another common way to write a function is in the form y = 3x +6. In this case, x and y are the variables, where x is the independent variable and y is the dependent variable. This simply means that making a change to x will result in a change to y. Both x and y are very common variables that are often used, but be aware that other variables may be used instead.