Long Multiplication with Large Numbers
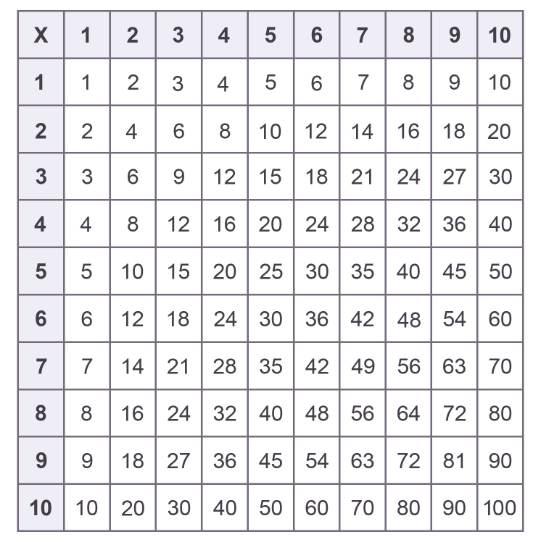
Now, if we would like to multiply, say, \(164 \times 9\), we can easily compute the long multiplication for smaller numbers based on our knowledge of the times table for the number 9. One can also multiply larger numbers using this same method, which just uses a few more steps. For example, we can multiply \(277 \times 84\). The simplest way to perform long multiplication is to write the long number first, then the smaller number directly underneath with their least significant digits aligned, then draw a horizontal line under that. The top number is named the multiplicand and the lower number is the multiplier (the number with more digits is usually selected as the multiplicand). The result of the multiplication is the product.
Example:
Multiply \(277 \times 84\) using long multiplication.
Solution:
\[ \begin{array}{r}
&277\\
\times \!\!\!\!\!\!&84\\
\hline
\end{array}
\]
To start the calculation, you multiply the last digit of the multiplicand, which is 7, by the last digit in the multiplier, the 4. This gives 28. You write the ones digit of 28, the 8, underneath the line in the end column. You write the tens digit of 28, the 2, above the multiplicand in the next column. Again, this is called carrying the 2 forward:
\[ \begin{array}{r}
&27^27\\
\times \!\!\!\!\!\!&84\\
\hline
&8\\
\end{array}
\]
Now, you move onto the next digit in the multiplicand, which is the 7, and you multiply this by the last digit in the multiplier, the 4. This gives 28, but you must add the 2 to 28 since you carried the 2 forward in the previous step, which gives us 30. Again, you write the ones digit of 30, the 0, underneath the line beside the 8 and you carry the 3 forward:
\[ \begin{array}{r}
&2^37^27\\
\times \!\!\!\!\!\!&84\\
\hline
&08\\
\end{array}
\]
Finally, you move on to the first digit in the multiplicand, the 2, and you multiply this by the last digit in the multiplier, the 4. This gives 8, but you must add the 3 to 8 since you carried a 3 forward in the previous step, which gives us 11. No need to carry anything as we have finished the calculation for the number 4 in the multiplier, so just write 11 down, but we are not finished:
\[ \begin{array}{r}
&2^37^27\\
\times \!\!\!\!\!\!&84\\
\hline
&1108\\
\end{array}
\]
Now, we basically start our multiplication over by moving onto the next digit in the multiplier, the 8. Before we do this, since we are moving onto the next digit in the multiplier, we must continue our multiplication on the next line, but first add a zero in the first digit, then draw a horizontal line under that:
\[ \begin{array}{r}&277\\
\times \!\!\!\!\!\!&84\\
\hline
&1108\\
&0\\
\end{array}
\]
(Notice that the numbers that were previously carried forward are now erased)
Now, you start over by multiplying the last digit of the multiplicand, which is 7 , by the next digit in the multiplier, the 8. This gives 56. You write the ones digit of 56, the 6, above the last line beside the 0 and you carry the 5 forward:
\[ \begin{array}{r}
&27^57\\
\times \!\!\!\!\!\!&84\\
\hline
&1108\\
&60\\
\end{array}
\]
Now, you move onto the next digit in the multiplicand, which is the 7, and you multiply this by the next digit in the multiplier, the 8. This gives 56, but you must add the 5 to 56 since you carried the 5 forward in the previous step, which gives us 61. Again, you write the ones digit of 61, the 1, above the last line beside the 6 and you carry the 6 forward:
\[ \begin{array}{r}
&2^67^57\\
\times \!\!\!\!\!\!&84\\
\hline
&1108\\
&160\\
\end{array}
\]
Finally, you move on to the first digit in the multiplicand, the 2, and you multiply this by the next digit in the multiplier, the 8. This gives 16, but you must add the 6 to 16 since you carried a 6 forward in the previous step, which gives us 22. No need to carry anything as we have finished the calculation for the number 8 in the multiplier, so just write 22 down, but we are still not finished:
\[ \begin{array}{r}
&2^67^57\\
\times \!\!\!\!\!\!&84\\
\hline
&1108\\
&22160\\
\end{array}
\]
Our final step is to simply add the final two numbers obtained from the multiplication:
\[ \begin{array}{r}&277\\
\times \!\!\!\!\!\!&84\\
\hline
&1108\\
+&22160\\
\hline
&23268
\end{array}
\]
Example 1:
Example 2:
Example 3:
