Antiderivatives

Introduction

Derivatives involve finding the rate of change of a function. But what if you were given the rate of change and wanted to know the original function? Well, the process of going from the derivative function to the original is called antidifferentiation; i.e., we find the antiderivative of the given function. Basically, derivatives and antiderivatives undo one another (they are inverse processes).

WHAT DOES THIS MEAN?

If you’re given a function and asked for its antiderivative, you just have to ask yourself, “I’m looking for a function whose derivative is ____ (given)…what function satisfies that criteria?” Let’s say you want to know the anti-derivative of $2x.$ You ask yourself, “What function, when I differentiate it, will give me $2x$?” Well, $x^2$ satisfies the criteria, so this means that an anti-derivative of $2x$ is $x^2$.

THE CONSTANT OF INTEGRATION

Technically, there’s an entire family of functions that are antiderivatives to a given function. Let’s go back to the above example, where we want to find the antiderivative of $2x$… sure, $x^2$ satisfies the criteria, but so does $x^2+2$ or $x^2-100$… all of these have a derivative of $2x$ because, upon differentiating, the derivative of a constant is 0. So we write that the general antiderivative of $2x$ is $x^2+C$, where C is called the constant of integration.

This is illustrated graphically in the figure below, where the red line denotes the function $2x$, and the green lines denote the family of antiderivatives, which are of the form $x^2+C$ (parabolas shifted vertically). The blue curve is just an example of an antiderivative (in this case $x^2$).

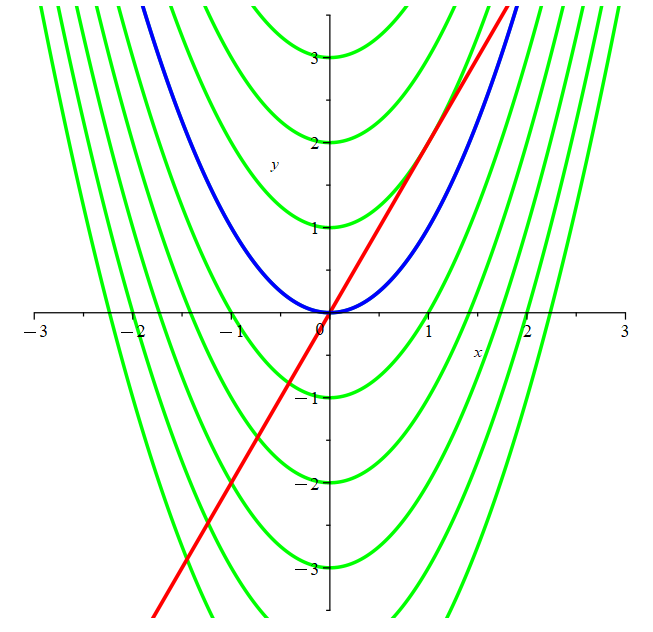
$antiderivatives$

NOTE: If you were given some sort of initial condition, then you could use that to solve for the value of the constant.

NOTATION

You might see different notation for antiderivatives. Often, we denote the antiderivativeof a function with the same letter, but using a capital. In the example above, we’d say that if $f(x) = 2x$, then $F(x)=x^2$ and then the most general antiderivative is $F(x) + C$, which is $x^2+C$.

Aside:

Alternatively, if you’re taking a calculus class, you might find antiderivatives referred to as “indefinite integrals”, and the notation is then $\int{2xdx}=x^2+C$ where the integration sign in front and the “dx” are just part of the notation.

RULES FOR FINDING ANTIDERIVATIVES

First of all, the following 2 properties (similar to what we had when we found derivatives) are helpful:

If $F(x)$ is an antiderivative of $f(x),$ then $kF(x)$ is an antiderivative of $kf(x)$.
If $F(x)$ is an antiderivative of $f(x)$ and $G(x)$ is an antiderivative of $g(x)$, then $F(x)\pm G(x)$ is an antiderivative of $f(x) \pm g(x)$.

.Additionally, the following table gives several useful antiderivatives.

Antiderivatives
$f(x)$	$F(x)$	$f(x)$	$F(x)$
$x^n$ (for n≠ -1)	$\frac{x^{n+1}}{n+1}$	$\sec^2 x$	$\tan x$
$\frac{1}{x}$	$\ln \|x\|$	$\sec x \tan x$	$\sec x$
$e^x$	$e^x$	$\frac{1}{\sqrt{1-x^2}}$	$\sin^{-1} x$
$\sin x$	$-\cos x$	$\frac{1}{1+x^2}$	$\tan^{-1} x$
$\cos x$	$\sin x$

CHECKING YOUR WORK

Because differentiation and antidifferentiation “undo” one another, you can check your work by differentiating! i.e., Find the derivative of what you got for F(x), and you should get back the original function in the question, f(x)!!

Example:

Find the antiderivative of $f(x)= x^2 - 6x +1$

Solution:

$F(x) = \frac{1}{3}x^3 - 3x^2 + x + C$

Example:

Find the antiderivative of $f(x) = 7\cos(x) -\frac{2}{x} + 9e^x$

Solution:

$F(x) = 7\sin{x} - 2\ln{|x|} + 9e^x + C$

Example:

Find the antiderivative of $f(x) = \frac{1}{x^3} + \sqrt{x} + 8$.

Solution:

$ f(x) = x^{-3} +x^{1/2} + 8$

$F(x) = -\frac{1}{2}x^{-2} + \frac{2}{3}x^{3/2} + 8x + C $

Example 1:

Example 2:

\(f(x)\)	\(F(x)\)	\(f(x)\)	\(F(x)\)
\(x^n\) (for n≠ -1)	\(\frac{x^{n+1}}{n+1}\)	\(\sec^2 x\)	\(\tan x\)
\(\frac{1}{x}\)	\(\ln \|x\|\)	\(\sec x \tan x\)	\(\sec x\)
\(e^x\)	\(e^x\)	\(\frac{1}{\sqrt{1-x^2}}\)	\(\sin^{-1} x\)
\(\sin x\)	\(-\cos x\)	\(\frac{1}{1+x^2}\)	\(\tan^{-1} x\)
\(\cos x\)	\(\sin x\)