Inverse Functions
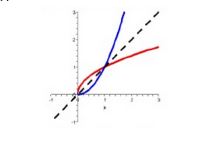
The inverse of a function results when we have solved for x as the dependent variable and y as the independent variable and have renamed them according to the usual convention. For example, if f(x) gives the number of bacteria in a culture as a function of time (time is the independent variable and bacteria is the dependent variable), then f -1(x) gives the time it takes for the number of bacteria in the culture to reach a certain value (bacteria is now the independent variable, and time is the dependent variable). The inverse function is denoted as f -1(x) and is read "f inverse". Graphically, it's the mirror image of the given function around the line y = x.
Existence
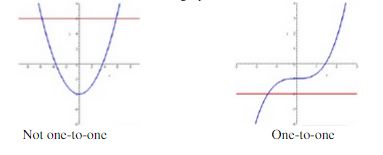
For a function to have an inverse, the function must be one-to-one. This simply means that f can never take on the same value twice (i.e., that no two values produce the same f(x) value). The horizontal line test states that a function is one-to-one if and only if a horizontal line cannot intersect its graph more than once.
Domain and Range
The inverse function has a domain that is equivalent to the original function's range and a range that is equivalent to the original function's domain; therefore, if a function has a domain of A and a range of B, then the inverse function would have a domain of B and a range of A. This makes sense since we can think of an inverse as 'flipping' the function around the line y = x, so that all the x and y values get swapped.
Finding an Inverse
To find the inverse of a one-to-one function, just follow the easy steps below:
- write the equation replacing f(x) with y;
- solve for x in terms of y;
- interchange x and y; and
- replace y with f -1(x).
In the above procedure, note that the order of the 2nd and 3rd steps can be interchanged.
One last thing to note about functions and their inverse is that the two cancel each other out. Therefore,
f(f -1(x)) = x and f -1(f(x)) = x
These are "cancellation equations" since one function undoes what the other did.
Example: Find the inverse of f(x) = (x - 3) ÷ 4
Solution:
Rewrite using y instead of f(x): y = (x - 3) ÷ 4
Isolate for x:
4y = x - 3
4y + 3 = x
Switch x and y and replace y with f -1(x): f -1(x) = 4x +3
Example: Given f(x) = 9 ÷ (x - 2), find f -1(x) and its domain and range.
Solution:
Rewrite using y instead of f(x): y = 9 ÷ (x - 2)
Isolate for x:
y(x - 2) = 9
x - 2 = 9/y
x = 9/y + 2
Switch x and y and replace with f -1(x): f -1(x)= 9/x + 2
The domain of f(x) is x ≠ 2, x ∈ R. Since the domain of the original is the range of the inverse, the range of f -1(x) is y ≠ 2, y ∈ R. The range of f(x) is y ≠ 0, y ∈ R; therefore, the domain of f -1(x) is x ≠ 0, x ∈ R.
Example: