Circles

INTRODUCTION

Here are a few quick facts that are useful to know about a circle that has radius r:

      

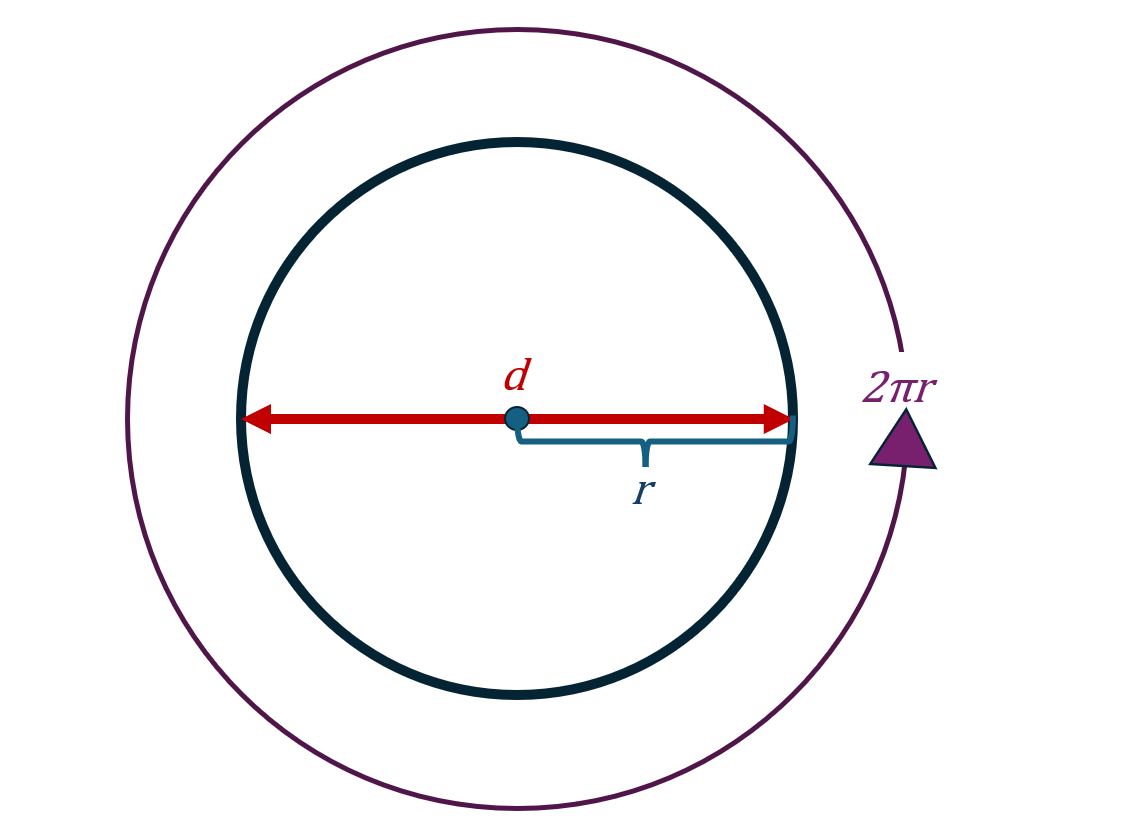
Diameter = 2r
Circumference = 2π r
Area = πr²

 

 

Example: If a circle has an area of 16π, what is its radius?

Solution: 

\(\displaylines{A = \pi r^2~ \text{but we have} ~A=16\pi ~\text{so} ~\pi r^2 = 16\pi \\ r^2 = 16 \\ r = 4}\)

 

THE EQUATION OF A CIRCLE

A circle with radius r centred at the origin has the equation:

\(x^2+y^2=r^2\)

A circle whose centre is at the point (a,b) has the equation:

\( (x-a)^2+(y-b)^2=r^2 \)

Example: Consider the circle given by the equation  \( (x - 3)^2 + (y + 2)^2 = 49\)

What is the position of it's centre? What is the radius?

Solution:

The centre is at \((3, -2)\).

The radius is 7.