Transformations of Exponential and Logarithmic Functions

The transformation of functions includes the shifting, stretching, and reflecting of their graph. The same rules apply when transforming logarithmic and exponential functions.

Vertical and Horizontal Shifts

Suppose c > 0. To obtain the graph of:

y = f(x) + c: shift the graph of y= f(x) up by c units

y = f(x) - c: shift the graph of y= f(x) down by c units

y = f(x - c): shift the graph of y= f(x) to the right by c units

y = f(x + c): shift the graph of y= f(x) to the left by c units

Example: The graph below depicts g(x) = ln(x) and a function, f(x), that is the result of a transformation on ln(x). Which of the following functions represents the transformed function (blue line) on the graph?

A. \(f(x)=\ln(x)+2\) 
B. \(f(x)=\ln(x)-2\)
C. \(f(x)=\ln(x-2)\)
D. \(f(x)=\ln(x+2)\)

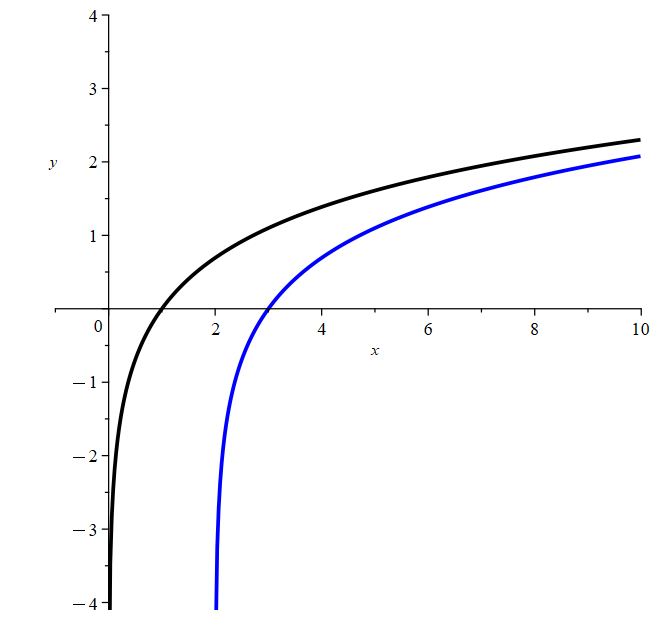
Solution: The correct answer is C. The curve is shifted to the right.

Vertical and Horizontal Stretches/Compressions

Suppose c > 1. To obtain the graph of:

y = cf(x): stretch the graph of y = f(x) vertically by a factor of c.

y = 1/c f(x): compress the graph of y = f(x) vertically by a factor of c

y = f(cx): compress the graph of y = f(x) horizontally by a factor of c

y = f(x/c): stretch the graph of y = f(x) horizontally by a factor of c

Example: Which curves do the following functions correspond to if black curve represents \(e^x\)? 

A. \( f(x)=e^{5x}\)

B. \( f(x)=e^{\frac{x}{5}}\)

 

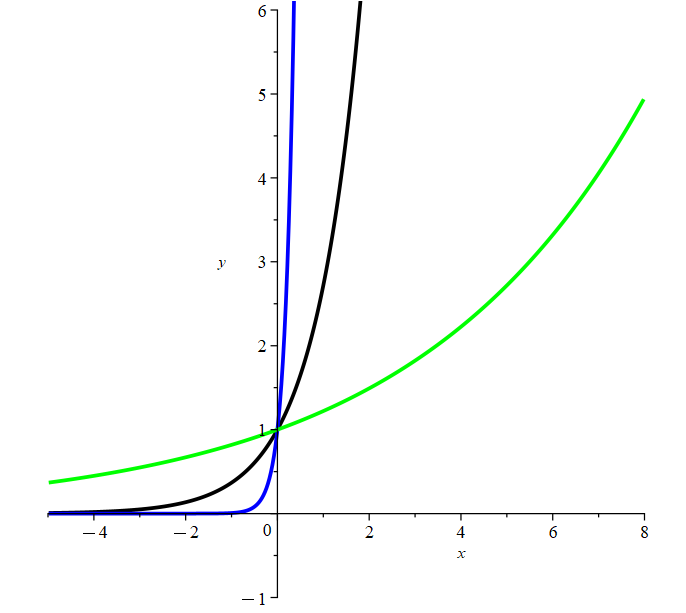
Solution: The blue curve matches function A. It is compressed horizontally by a factor of 5. The green curve matches function B. It is stretched horizontally by a factor of 5.

Reflections

To obtain the graph of

y= -f(x): reflect the graph of y = f(x) about the x-axis

y= f(-x): reflect the graph of y = f(x) about the y-axis

Example: Sketch the graphs of f(x) = ln(x), g(x) = ln(-x), and h(x)= -ln(x).

 Solution:

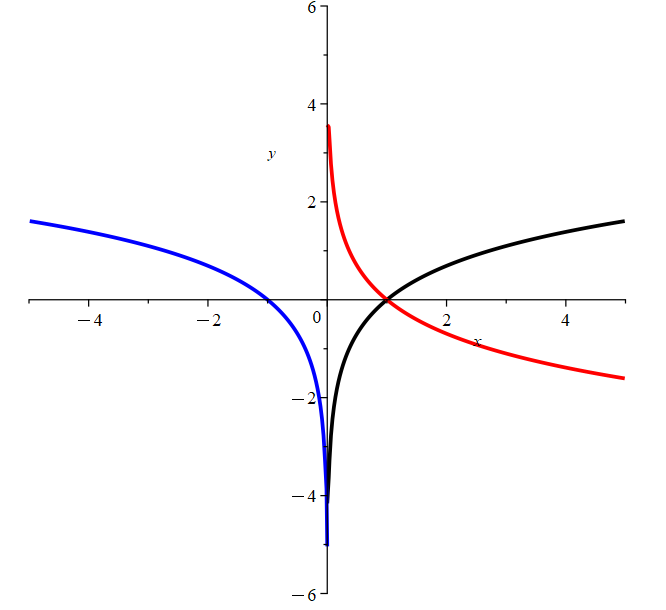
The black curve is the original, \(f(x)=\ln(x)\).

The blue curve is the reflection about the y-axis, \(g(x)=\ln(-x)\).

The red curve is the reflection about the x-axis, \(h(x)=-\ln(x)\).

 

Transformation of Exponential Functions Example:

Transformation of Logarithmic Functions Example: