Domain and Range of Exponential and Logarithmic Functions

The domain of a function is the specific set of values that the independent variable in a function can take on. The range is the resulting values that the dependant variable can have as x varies throughout the domain.

Finding the domain/range

When determining domain it is more convenient to determine where the function would not exist. For example, we can only take the logarithm of values greater than 0. However, its range is such that y ∈ R. Remember that logarithmic functions and exponential functions are inverse functions, so as expected, the domain of an exponential is such that x ∈ R, but the range will be greater than 0.

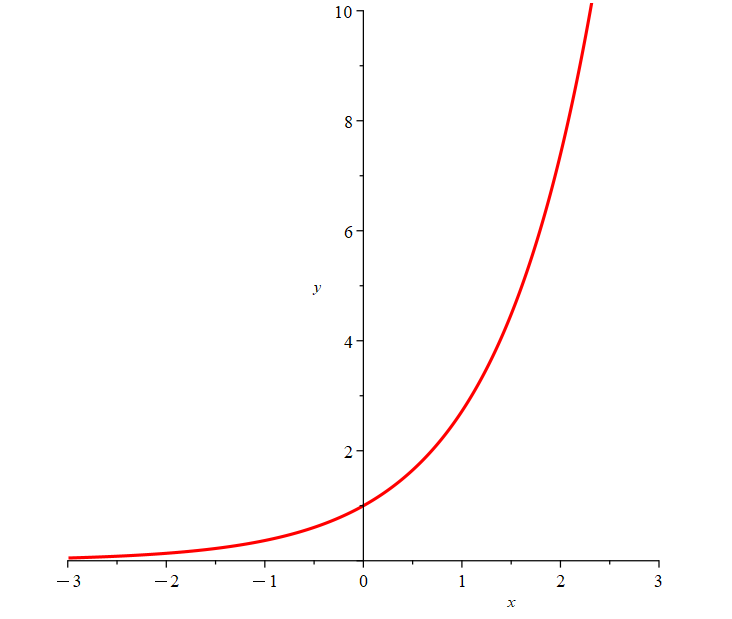
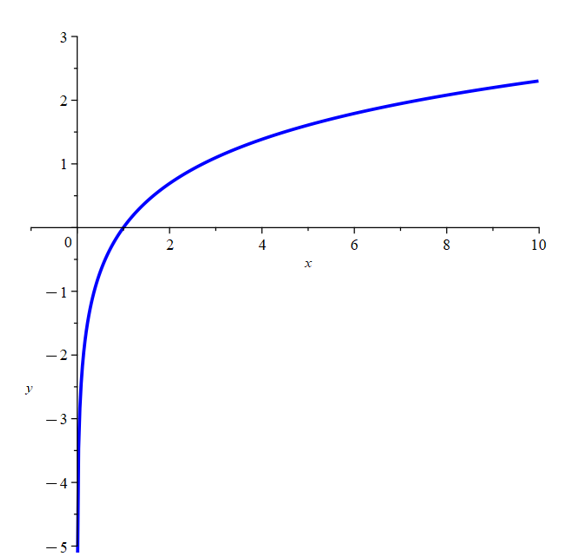
$graph of e^x$ $graph of ln(x)$

$f(x)=e^x$ $f(x)=\ln (x)$

Example: Find the domain and range for $f(x)=\ln (x+5)$

Solution:

Domain Range

$x + 5 > 0$ y ∈ R

$ x > -5 $

Example: Find the domain and range for $f(x) = \frac{1}{e^x-1}$

Solution:

Domain Range

$e^x-1\neq0$ $y \neq 0$

$e^x\neq1$

$\ln (e^x) \neq \ln (1) $

$ x \neq 0 $

Example 1:

Example 2: