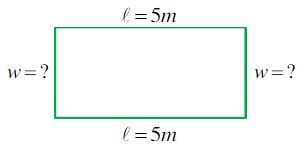Word Problems
This is a guide on how to solve word problems!
Definition of a Word Problem:
Before you start to solve word problems, it is important to understand what a word problem is. A word problem is a mathematical exercise which is in the form of a hypothetical question that needs mathematical analysis and equations to be solved. A good way to solve word problems is by using the method called “GRASS.” GRASS is an acronym for Given, Required, Analysis, Solution, and Statement. You can use GRASS, step by step, to break down a word problem, making it easier to solve.
GRASS:
Given: Identify the given information in the question. What values are given and what do they represent? It may be helpful to know the following terms that are sometimes used in math questions and what they mean:
|
Term |
Meaning |
|
Sum |
+ (addition) |
|
Difference |
- (subtraction) |
|
Product |
* (multiplication) |
|
Quotient |
/ (division) |
Required: Look at what the question is actually asking you to find. Whatever it is, represent it with a variable e.g., x.
Analysis: If applicable, draw a sketch if one is not already provided. Decide on the appropriate math techniques to use and the formulas that relate the different quantities of interest. Whenever possible, use one variable only. For example, if you're looking for two numbers that differ by 5, then let x, and x+5 (or x and x-5) represent the two numbers, NOT x and y. Alternatively, you may be able to use some information presented in the question to help you rewrite your equation in terms of one variable only.
Solution: Solve the equation or find the answer you're looking for. You’ll have to think hard about the various math techniques you’ve learned in your courses to figure out which ones work for this particular question. Make sure your solution(s) makes sense in the context of the application—e.g., a negative area doesn't make any sense.
Statement: Finish off with a concluding statement to make clear the answer to the question. If applicable, include units in your answer.
Here is a simple example to show how GRASS is used to solve a word problem.
Example:
The perimeter of a rectangular park is 26 m. If the length of the park is 5m, what is the width of the park?
Given: In this question, we are given the perimeter of the rectangular park as 26 m. We are also told that the length of the park is 5 m. So, P= 26m and L= 5m.
Required: The question asks: “What is the width of the park?” From this we know we have to find the width. Find: w = ?
Analysis: We can draw a sketch of the rectangular park to find out what formulas we might have to use to find the width.
Note: The longer sides are the lengths and the shorter sides are the widths.
So from this sketch, we can see that we need the formula for the perimeter of a rectangle.
P= 2L + 2w
If we rearrange the equation for w, then we get
w = (P – 2L) ÷ 2
The simplified equation is,
w = P/2 - L
Solution: So now that we have our equation, we can solve for the unknown variable w by subbing in our known variables, P and L.
w = (26m)/2 - 5m
w = 13m - 5m
w = 8m
Statement: We found that the width is 8 metres. So now write your final answer from your solution in words.
Therefore, the width of the rectangular park is 8 metres.
Example:
Example:
Example: