Introduction to Trigonometric Functions

Let's review some background material to help us study trigonometric functions.

DEFINITIONS

First, let's start by looking at what these functions look like... the one's we'll use most frequently are \(\sin\theta\), \(\cos \theta\), and \(\tan \theta\), where \( \theta\) is commonly used as the independent variable  when dealing with trig functions.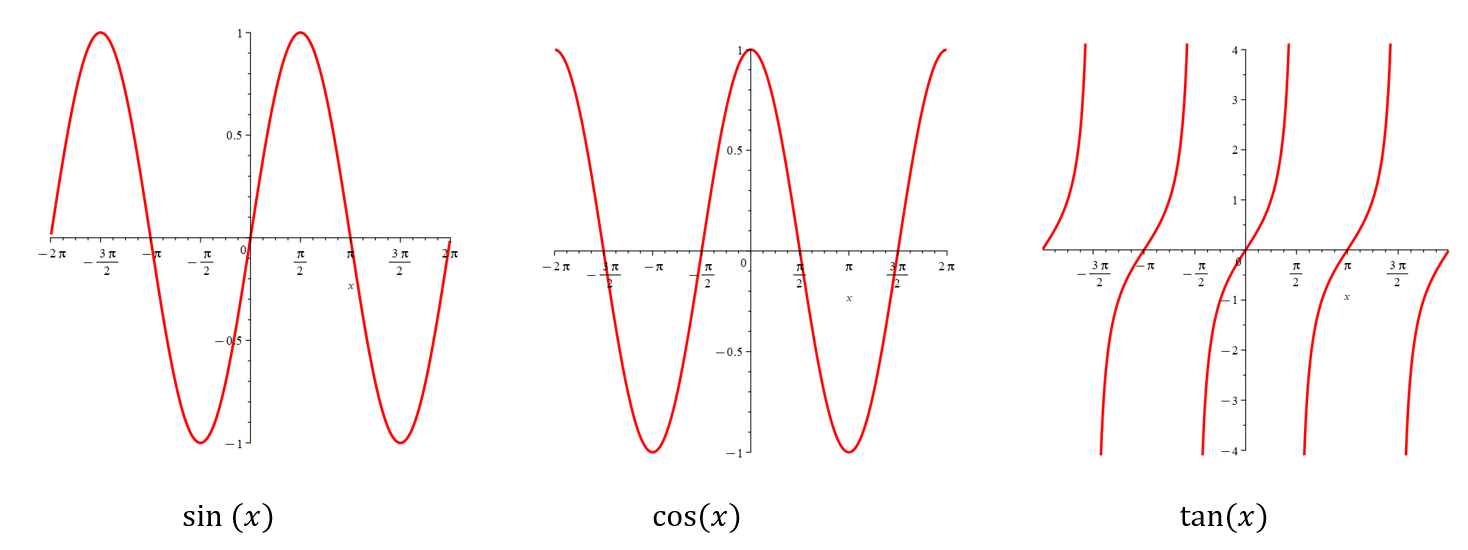



In addition, there are other useful trigonometric functions that are important in many applications. We can describe these in terms of sine and cosine.
\[\tan\theta = \frac{\sin\theta}{\cos\theta} \quad \quad \quad   \cot\theta = \frac{\cos\theta}{\sin\theta}\] 
\[\csc\theta = \frac{1}{\sin\theta} \quad \quad \quad   \sec\theta = \frac{1}{\cos\theta}\]
Based on the above definitions, we can evaluate these trigonometric functions at particular angles if we know the sine and cosine of those angles.

PERIODICITY

The trigonometric functions are periodic functions (their pattern repeats). A function \(f\) is called periodic if \(f(x+p) = f(x)\) for all \(x\) in the domain where, where \(p\) is a positive constant; the smallest such value of \(p\) is called the period. Both \(\sin\theta\) and \(\cos\theta\) have a period of \(2\pi\), while \(\tan\theta\) has a period of \(\pi\).