Composition of Functions

The composition of two functions \(f\) and \(g\) is the new function \(h\), where \(h(x) = f(g(x))\), for all \(x\) in the domain of \(g\) such that \(g(x)\) is in the domain of \(f\). The notation for function composition is \(h = f \circ g\) or \(h(x) = (f \circ g)(x)\) and is read as 'f of g of x'. The procedure is called composition because the new function is composed of the two given functions \(f\) and \(g\), where one function is substituted into the other.

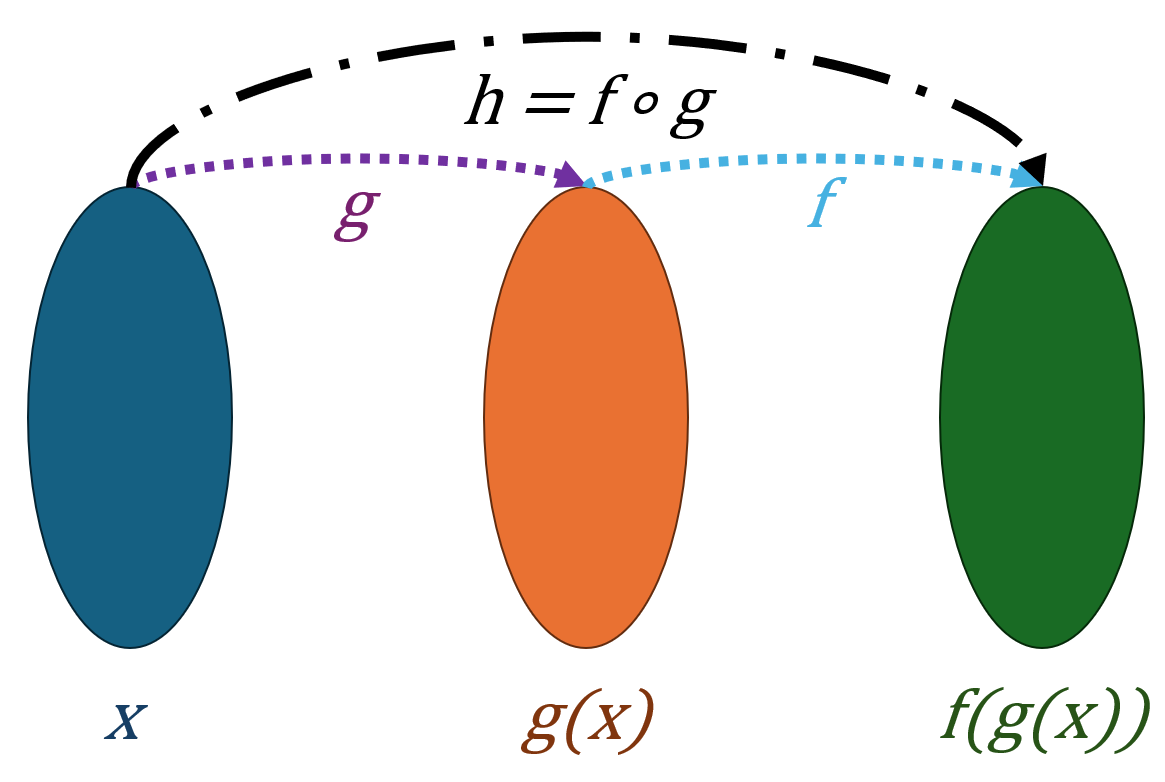
Finding the Composition

Although composition of functions is best illustrated with an example, let us summarize the key steps:

• rewrite \(f \circ g\) as \(f(g(x))\);
• replace \(g(x)\) with the function that it represents;
• evaluate \(f\) by replacing every \(x\) with the function that \(g(x)\) represents; and
• finally, if given a numerical value of \(x\), evaluate the new function at this value by replacing all remaining \(x\) with the given value.

Note: Often \(f \circ g \neq g \circ f\) and the two will have different domains. Also, be aware that you can take the composition  of more than two functions: e.g., \(f(g(k(x)))\).

Example: Given the function \(f(x) = x^2\) and \(g(x) = x + 3\), find \(f(g(1))\) and \(g(f(1))\).

Solution:

\begin{align*} f(g(x)) &= f(x + 3)                   &  &  &         g(f(x)) &= g(x^2)\\&= (x +3)^2          &  &   &      &= x^2 + 3\\f(g(1)) &= (1 + 3)^2    &  &  &        g(f(1))& =1^2 + 3\\ &=16       &   &   &        &=4\end{align*}

 

 Notice that \( f \circ g \neq g \circ f \).

Composition of Function Example 1:

Composition of Function Example 2:

Composition of Function Example 3: