Piecewise-Defined Functions

A piecewise function exists when a function is defined by two or more different functions throughout its domain. The first step in evaluating a piecewise function is to determine which function definition applies depending on the value of x that is being input. Once that has been determined, we evaluate the function as usual by substituting in the given value of x.

Example:

Given $f(x) =
\left\{
\begin{array}{lr}
-x&\text{if}~x<0\\
x^2+1&\text{if}~x\ge0
\end{array}
\right\}$,find $f(-1)$, $f(0)$ and $ f(1) $

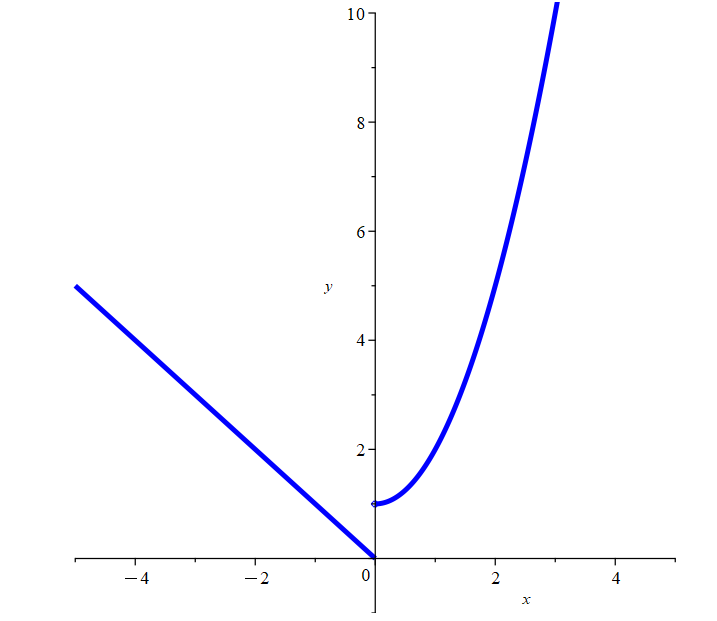
$piecewise function$

Solution: First, we want to evaluate $f$ at $x=-1$, so $f(x)=-x$ is the equation to use

(since it applies whenever $x<0$).

$ \displaylines{
f(x) &=& -x \\
f(-1) &=& -(-1) \\
f(-1) &=& 1} $

Next, we want to evaluate $f$ at $x=0$, so $f(x)=x^2+1$ is the equation to use.
(Since it applies whenever $x\geq 0$.)

$\displaylines{f(x) &=& x^2+1 \\ f(0) &=& 0^2+1 \\ f(0) &=& 1} $

Finally, we evaluate $f$ at $x=1$, so $f(x)=x^2+1$ is the equation to use. (Since it applies whenever $x\geq 0$.)

$\displaylines{f(x) &=& x^2+1 \\ f(1) &=& 1^2+1 \\f(1) &=& 2} $

Absolute Value Functions

An absolute value function can be rewritten as a piecewise function. Absolute value is the distance from a number 'x' to 0 on the real number line. Therefore, when the value of a function is equal to zero or is positive, taking its absolute value doesn't change it; however, if the value is negative, taking absolute value changes the sign. Therefore, the definition of the function changes depending on whether or not x ≥ 0.

$y = |x| = \begin{cases} x & \text{if } x \geq 0 \\ -x & \text{if } x < 0 \end{cases} $

Example: Write $y = |x-2|$ as a piecewise function and evaluate $f(0)$, $f(2)$, and $f(5)$.

Solution:

$ f(x) = \begin{cases} x-2, & \text{if } x \geq 0 ~or~x\geq 2 \\ -(x-2), & \text{if } x < 0~or~x<2 \end{cases} $

First, to find $f(0)$, we use $f(x) = -(x-2)$, since this applies when $x<2$:

$ \displaylines{f(x) &=& -(x-2) \\ f(0) &=& -(0-2) \\ f(0) &=& 2} $

Next, to find $f(2)$, we use $f(x) = x-2$, since this applies when $x \geq 2$:

$ \displaylines{f(x) &=& x-2 \\ f(2) &=& 2-2 \\ f(2) &=& 0} $

Finally, to find $f(5)$, we use $f(x) = x-2$, since this again applies when $x \geq 2$:

$ \displaylines{f(x) &=& x-2 \\ f(5) &=& 5-2 \\ f(5) &=& 3} $

Example 1:

Example 2:

Example 3: