Domain and Range of Trigonometric Functions
QUICK DOMAIN/RANGE REVIEW
The domain of a function is the specific set of values that the independent variable in a function can take on. The range is the resulting values that the dependant variable can have as \(x\) varies throughout the domain.
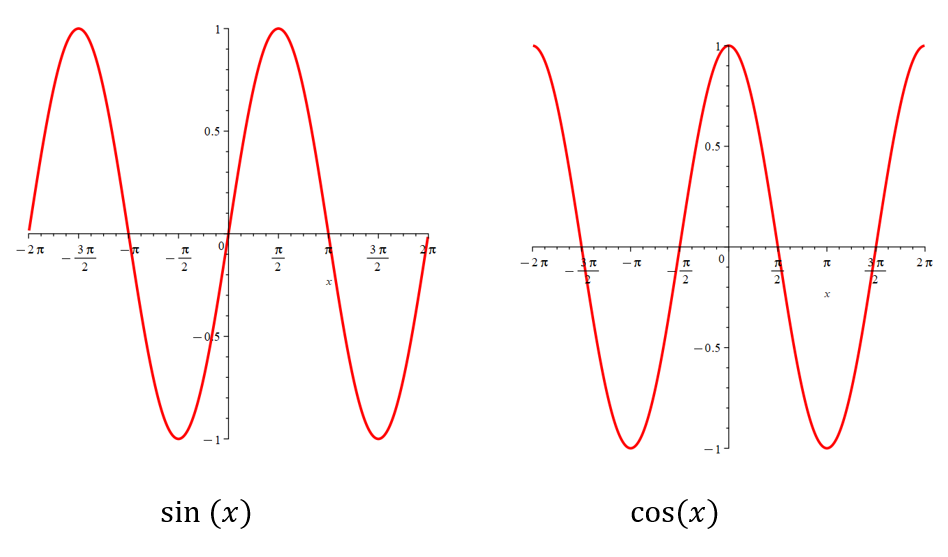
DOMAIN AND RANGE FOR SINE AND COSINE FUNCTIONS
There are no restrictions on the domain of sine and cosine functions; therefore, their domain is such that \(x \in \mathbb{R}\). Notice, however, that the range for both \( y = \sin(x)\) and \(y = \cos(x)\) is between -1 and 1. Therefore, transformations of these functions in the form of shifts and stretches will affect the range but not the domain.
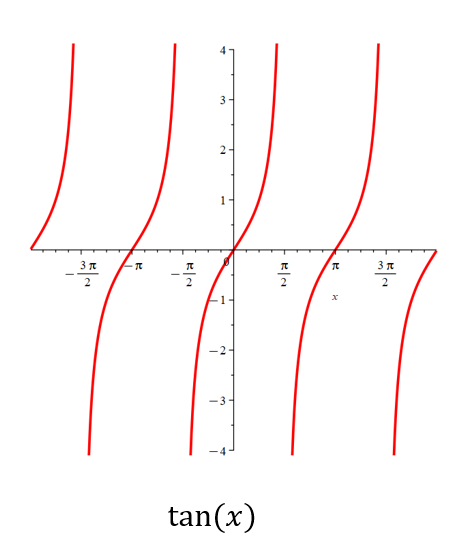
DOMAIN AND RANGE FOR THE TANGENT FUNCTION
Notice that \(y = \tan(x)\) has vertical asymptotes at \(x=\pm \frac{(2n+1)\pi}{2}\). Therefore, its domain is such that \( x \neq \pm \frac{(2n+1)\pi}{2}\). However, its range is such that \( y \in \mathbb{R}\), because the function takes on all values of \(y\). In this case, transformations will affect the domain but not the range.
Example: Find the domain and range of \(y = \cos(x) - 3\).
Solution:
Domain: \(x \in \mathbb{R}\)
Range: \(-4 \le y \le -2, y \in \mathbb{R}\)
Notice that the range is simply shifted down 3 units.
Example: Find the domain and range of \(y = \cos(x) - 3\)
Solution:
Domain: \( x \neq \pm \frac{(2n+1)\pi}{2}, x \in \mathbb{R}\)
Notice that the domain is the same as the domain for \( y = \tan(x)\) because the graph was stretched vertically—which does not change where the vertical asymptotes occur.
Range: \(y \in \mathbb{R}\)
