Vector Addition, Subtraction, and Scalar Multiplication

MULTIPLICATION BY A SCALAR

Suppose we multiply by a scalar number $c$ and we get:

a compression if $-1 < c < 1$;
a stretch if $c > 1$ or $ c < -1$; or,
if $c$ is negative then the direction of the vector flips $180^{\circ}$.

In the diagram below, the initial vector $\boldsymbol{V}$ is shown in black. The vector $-2\boldsymbol{V}$ is shown in green.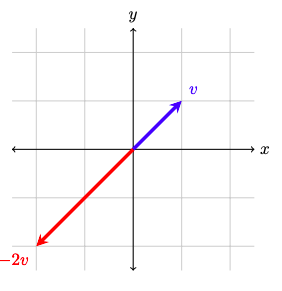
$vector multiplied by a scalar$

Algebraically, to multiply a vector by a scalar (i.e. number) $c$, you simply multiply each component of the vector by $c$.

Example: If $\overrightarrow{v} = <-1,3>$, find $-5\overrightarrow{v}$.

Solution: \[\begin{equation}
\begin{split}
-5\overrightarrow{v} & = -5<-1,3> \\
& = <-5(-1),-5(3)>\\
& = <5,-15>\\
\end{split}
\end{equation}\]

VECTOR ADDITION AND SUBTRACTION

To find the sum of two vectors, we place the initial point of the 2nd vector
at the terminal point of the 1st vector. This is shown graphically in the image below.

Here, we’re adding the blue vector (let’s call it $\boldsymbol{A}$) and the red vector (let’s call it $\boldsymbol{B}$) together. Note that we can add $\boldsymbol{A} + \boldsymbol{B}$ or $\boldsymbol{B} + \boldsymbol{A}$ and we obtain the same result, which is a new vector shown in black.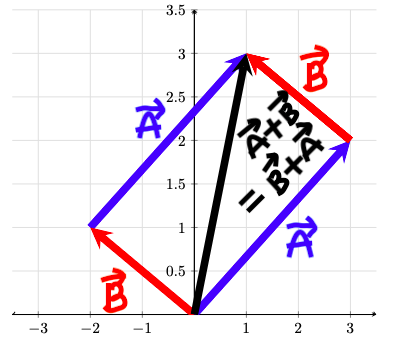

$vector addition$

To subtract vectors, i.e., to find $\boldsymbol{A} - \boldsymbol{B}$, we can simply find the sum $\boldsymbol{A} + (-\boldsymbol{B})$.
Algebraically, we just add or subtract each component of the 2nd vector to/from the corresponding components of the 1st vector.

Example: If $\overrightarrow{u} = <4,-2>$ and $\overrightarrow{v} = <-1,7>$, find $\overrightarrow{u} + \overrightarrow{v}$.
Solution: \[\begin{equation}
\begin{split}
& = \overrightarrow{u} + \overrightarrow{v}\\
& = <4,-2> + <-1,7> \\
& = <4 + (-1), -2 + 7>\\
& = <3 ,5 >
\end{split}
\end{equation}\]

Example: