Balancing equations

Chemical reactions are represented by balanced chemical equations, which show the molecules that are reacting on the left side and the molecules that are produced on the right side. We have to make sure that the reactant and product sides have identical amounts of atoms – for example, if we react molecules containing 2 atoms of hydrogen then we must produce molecules that have 2 atoms of hydrogen as well. This is known as the law of conservation of mass: matter cannot be created or destroyed.

As an example, let’s look at the unbalanced reaction of water (H₂O) with sodium (Na):

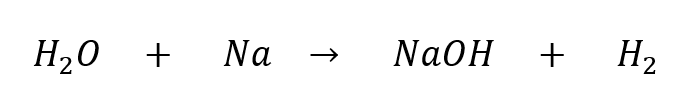
There is a problem, because the left side has 2 hydrogen atoms but the right side has 3. To fix this, we can change the coefficients that come before the molecules. We can’t change the subscripts (for example, we can’t change the 2 in H₂O). The correct balanced equation looks like this:

We had to add three new coefficients to balance the equation. Now we have 4 hydrogens on the left and 4 hydrogens on the right. Don’t forget that when you are counting atoms that you must multiply the molecule’s coefficient with the atom’s subscript – in this case, 2 H₂O has 4 H total because each individual H₂O molecule has 2 H.

Basic steps for balancing equations

1. Count all the elements on both sides of the reaction. Note which elements are currently unbalanced.
2. Start by balancing elements that only appear in one molecule on each side. Do this by changing the coefficients, not the subscripts!
3. Double check the balance and note the new count of each element on both sides of the equation.
4. Balance the remaining elements.
5. Check that everything is balanced! Make sure you are taking into account the coefficients and the subscripts.

Tip: You can use fractions to help get the right ratio of atoms, but you must convert these to whole numbers before you finish balancing. You can eliminate fractions by multiplying the entire reaction by the denominator.

e.g. Let’s try balancing this equation using the above steps:

First: we count that the left side has 2 C, 6 H, and 2 O, while the right side has 1 C, 2 H, and 3 O. All three elements are unbalanced.

Second: we note that oxygen appears in two molecules on the right side, which makes it a bit trickier to balance, so we will save it for later. To balance the C and H atoms, we can change the coefficients of CO₂ and H₂O on the right side.

Third: we count our atoms again. The left side has 2 C, 6 H, and 2 O. The right side has 2 C, 6 H, and 7 O. The only element that is not balanced is O.

Fourth: we balance the oxygens. This is where the above tip about using fractions becomes useful, because we have 2 O on the left and 7 O on the right. We cannot multiply O₂ by a whole number to get 7, but we can multiply it by a fraction to get 7.

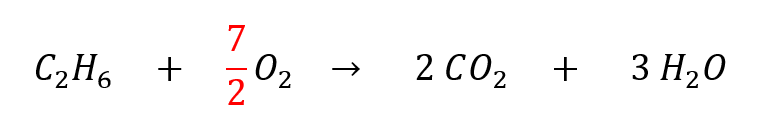
Now we have 7 oxygens on each side. However, we need all the coefficients to be whole numbers. We can fix this by multiplying the entire equation by the denominator (2) to get rid of the fraction:

Fifth: double check that all the elements have the same count on both sides. The left side and right side both have 4 C, 12 H, and 14 O, so we’re finished!